TABELA 1 - Equações utilizadas no método de Constantinou e Gani de estimativa de propriedades termofísicas. |
|
|
ESTIMATIVA DE PROPRIEDADES TERMOFÍSICAS
Propriedades termodinâmicas do gás perfeito: capacidade calorífica do gás perfeito (Cp0), entalpia de formação no estado padrão, (DHf 0), e
energia de Gibbs de formação (DGf 0)
INTRODUÇÃO
A necessidade de conhecer valores da capacidade calorífica do gás perfeito em função da temperatura é fundamental em várias áreas do conhecimento podendo
destacar-se a do ambiente, da combustão e de uma forma mais geral o domínio das reacções químicas onde é fundamental também o conhecimento da entalpia de
formação DHf 0 e da energia de Gibbs de formação DGf 0 dos compostos. O estado de referência para estas duas propriedades define-se através da temperatura de referência
(298.15 K) e com a pressão de referência que é uma atmosfera (=101325 Pa). A entalpia de formação define-se como a variação de entalpia para formar as espécies a partir
dos elementos nos seus estados padrão através de uma reacção química isotérmica. De maneira semelhante se define a energia de Gibbs de formação.
A entalpia de formação a 298.15 K, DHf 0(298.15K) e a energia de gibbs DGf
0(298.15) encontram-se tabeladas [1] para numerosas substâncias.
MÉTODOS
Os métodos de estimativa mais fiáveis para calcular DHf 0(298.15K), DGf 0(298.15) e Cp0 (T) baseiam-se em contribuição de grupos e foram desenvolvidos a partir da estrutura
molecular. Nestes métodos a estimativa daquelas propriedades derivam da soma de contribuições a grupos moleculares específicos retirados de tabelas. É o caso do método
de Constantinou e Gani [2,3] que se utiliza nesta applet JAVA e que constitui um método de contribuição de grupos aplicável à estimativa de várias propriedades de moléculas
orgânicas que podem ser de grande complexidade estrutural. Além da estimativa de DHf 0(298.15K), DGf 0(298.15) e Cp0 (T) o método de Constantinou e Gani aplica-se
também a Tfp a (temperatura de fusão), a Tb (temperatura de ebulição normal), Tc( temperatura crítica), Pc(pressão crítica), Vc(volume molar crítico), w (factor acêntrico de
Pitzer), DHv298 (entalpia de vaporização a 298 K), e Vliq,298 (volume molar do líquido a 298 K) (ver)
Para uma compreensão geral dos métodos recomenda-se a consulta da referência [4].
As equações do método incluem contribuições de primeira e de segunda ordem e estão indicadas na Tabela 1. Interessam aqui em particular as equaçoes de DHf 0(298.15K),
DGf 0(298.15) e Cp0 .
TABELA 1 - Equações utilizadas no método de Constantinou e Gani de estimativa de propriedades termofísicas. |
|
|
A equações dadas na Tabela 1 são da forma geral
onde:
Nk é o número de grupos de primeira ordem do tipo k na molécula;
F2j é a contribuição de primeira ordem do grupo j para a propriedade F;
Os métodos de primeira ordem envolvem o índice k enquanto as correções de (segunda ordem) envolvem o índice j. Sempre que é feito um cálculo de 1ª ordem utiliza-se W =0;
para incluir as correções faz-se W=1.
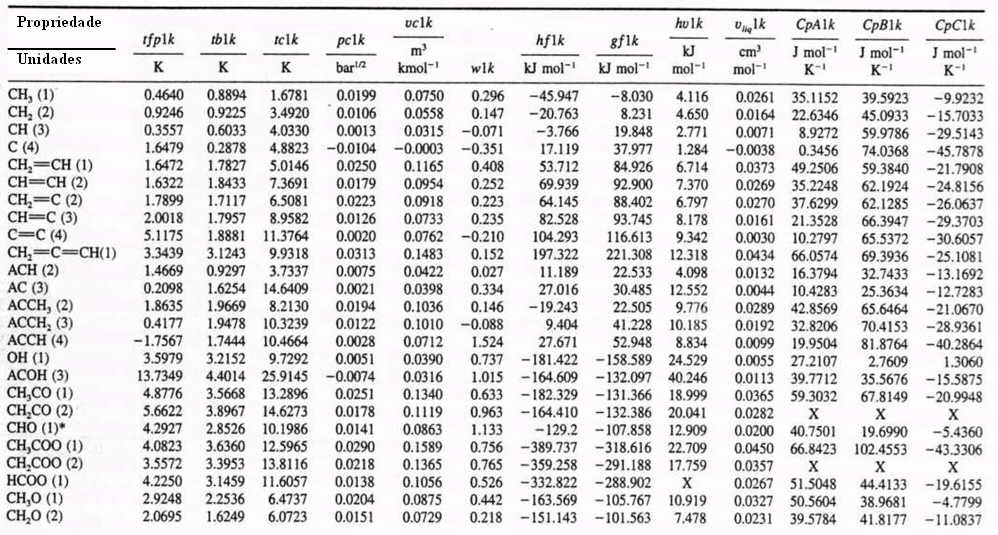
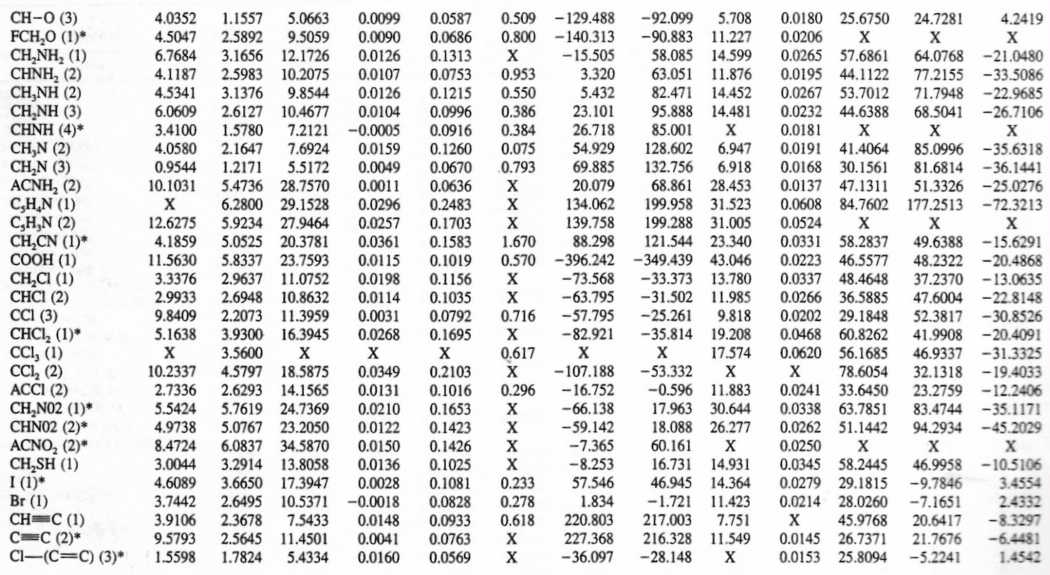
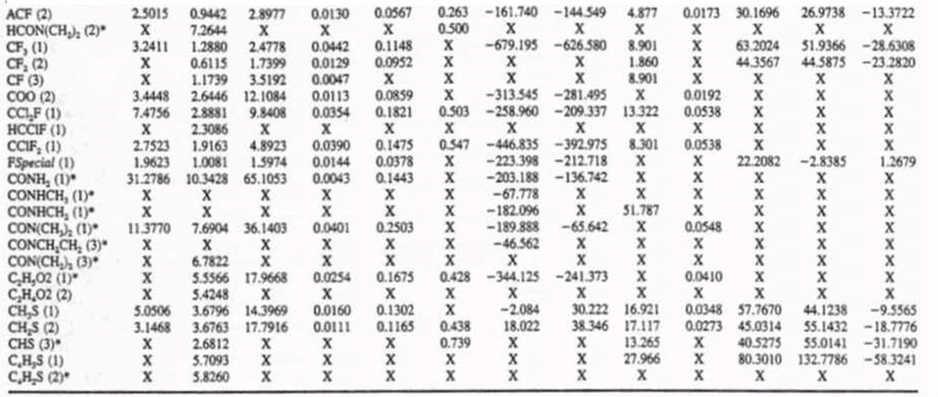
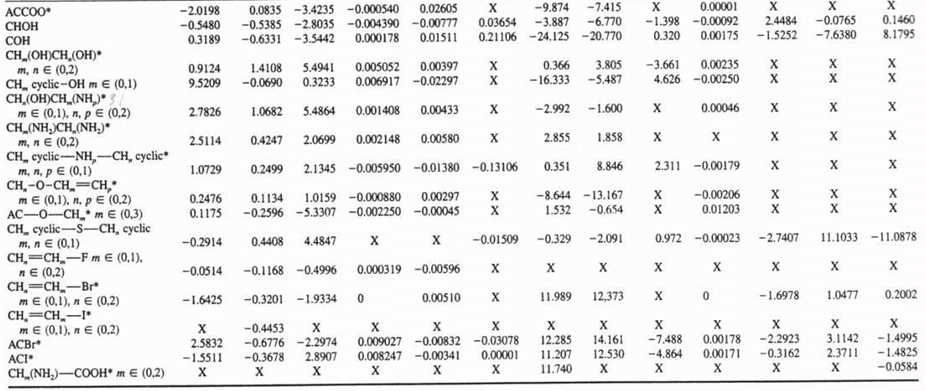
A tabela de contribuições dos grupos incluem 76 contribuições (grupos) de primeira ordem e 41 de segunda ordem. Na Tabela 2 mostram-se as contribuicões dos grupos de
primeira e de segunda ordem [1,2,3].
|
| TABELA 2 - Valores das contribuições de 1ª ordem para o método de Constantinou e Gani
|
 |
 |
 |
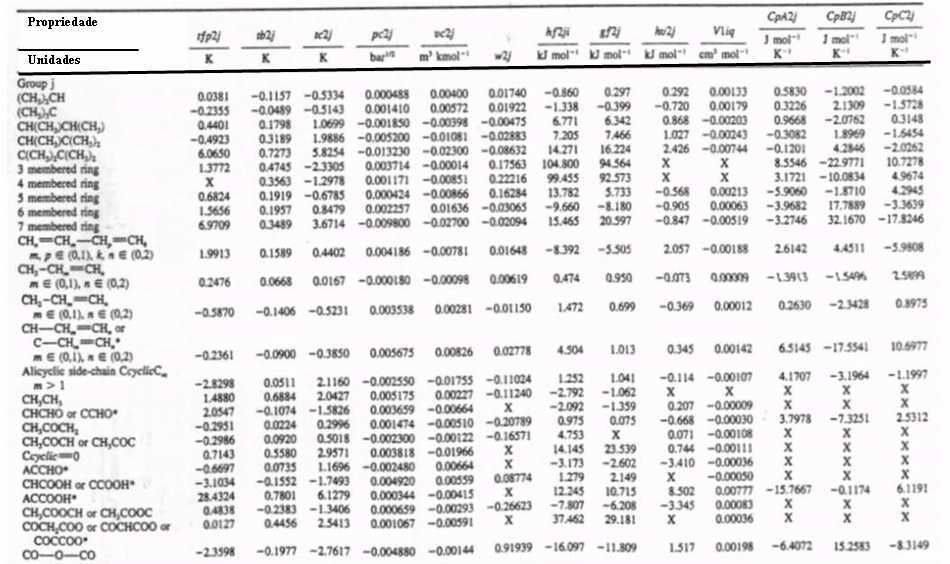
| TABELA 2 - Valores das contribuições de 2ª ordem para o método de Constantinou e Gani
|
 |
 |
O número de outros grupos a que cada grupo se encontra ligado é dado entre
parêntesis. Por exemplo o grupo CH2=CH(1) está ligado a 1 outro grupo,
CH=CH(2) e CH2=C(2) a
dois grupos e CH=C(3) a três grupos. AC designa um carbono aromático. Fspecial designa qualquer átomo de flúor que não se encontra em mais nenhum grupo.
Nos grupos das correcções de segunda ordem, as letras k, m, n e p referem-se ao número de átomos de hidrogénio que podem ser ligados a um átomo de carbono no grupo. O
seu número é dado num parêntesis seguido pelo símbolo. As ligações a outros carbonos ou outros átomos finalizam a coordenação. Por exemplo o grupo CH3-CHm=CHn, m Î
(0,1), n (0,2) corresponde ao desenvolvimento que se indica na tabela seguinte (Tabela 3). |
| TABELA 3 - Exemplo de desenvolvimento de grupos das correcções de 2ª
ordem. m n CH3-CHm=CHn Nº de outros grupos ligados |
| 0 0 CH3-C=C< 3 1 0 CH3-CH=C< 2 | 0 1 CH3-C=CH- 2 1 1 CH3-CH=CH- 1 | 0 2 CH3-C=C=CH2 1 1 2 CH3-C=CH2 0
|
Na Tabela 4 estão indicados exemplos de moléculas onde se utiliza pelo menos uma contribuição de 2ª ordem.
| |
(CH3)2CH
(CH3)3C CH(CH3)CH(CH3) CH(CH3)C(CH3)2 C(CH3)2C(CH3)2 3 membered ring 4 membered ring 5 membereci ring 6 membered ring 7 membered rlng CHn=CHm-CHp=CHk
m, p Î (0,1), k, nÎ (0,2) CH3-CHm=CHn , m Î (0,1), n Î (0,2) CH2-CHm=CHn m Î (0,1), n Î (0,2) CH-CHm=CHn or C-CHm=CHn
m Î (0,1), n Î (0,2)
4-Metil-2-Penteno (2) Alicyclic side-chain CcyclicCm m > 1 CH3CH3 CHCHO or CCHQ CH3COCH2 CH3COCH or CH3COC Ccyclic=O ACCHO* CHCOOH or CCOOH ACCOOH* CH3COOCH or CH3COOC COCH2COO or COCHCOO or COCCOO
CO¾O¾CO ACCOO
Benzoato de Etilo
(1) CHOH COH CHm(OH)CHn(OH)
m, n Î
(0,2) CHmcyclic¾OH, m Î (0,1) CHn(OH)CHm(NHp),
m Î (0,1), n, p Î (0,2)
1-Amino-2-Butanol (1) CHm(NH2)CHn(NH2), m, n Î (0,2) CHmcyclic-NHp-CHncyclic, m, n, p Î
(0,1) Pirrolidina (1) CHn¾O¾CHm=CHp, m Î (0,1), n, p Î
(0,2)
AC¾O¾CHm, m Î
(0,3)
Etilfenileter (1) CHmcyclic¾S¾CHncyclic, m, n Î (0,1) CHn=CHm¾F, m Î (0,1), n Î (0,2) CHn=CHm¾Br, m Î (0,1), n Î
(0,2)
1-Bromo-1-propeno (1) CHn=CHm¾I,
m Î (0,1), n Î (0,2)
1-Iodo-1-propeno
(1) ACBr ACI* CHm(NH2)¾COOH, m Î (0,2) |
Ccyclic é um átomo de carbono num composto em anel. As contribuições 3-, 4-, 5-, 6- e 7- para os grupos em anel não se utilizam quando se usam carbonos aromáticos nas contribuições de 1ª ordem.
A
aplicação JAVA a seguir realiza o cálculo de DHf 0(298.15K), DGf
0(298.15) e Cp0
(T). Nas contribuições
de segunda ordem (de) significa ![]() . Por exemplo: n de (0,1) significa
. Por exemplo: n de (0,1) significa
n ![]() (0,1).
(0,1).
| As equações do método de Constantinou e Gani são:
Ver explicação dos símbolos no quadro a seguir à tabela 1. |
RESULTADOS
A aplicação do método de Constantinou e Gani conduz geralmente a boas previsões como evidenciam os resultados seguintes [4b]:
(i) Para DHf 0(298.15K), considerando um total de 279 substâncias testadas o desvio médio absoluto percentual (DMA %) obtido foi de 8 %. O número de substâncias com desvios superiores a 10 % é de 42 e com desvios < 5% é de 187. Aplicando as contribuições de 2ª ordem sempre que possível (a 93 compostos) obtém-se DMA = 5 %.
(ii) Para DGf 0(298.15) e para 266 substâncias testadas o desvio médio absoluto percentual (DMA %) é de 12 %. O número de substâncias com desvios superiores a 10 % é de 75 e com desvios < 5% é de 135. Aplicando as contribuições de 2ª ordem sempre que possível (a 74 compostos) obtém-se DMA = 10 %.
(iii) Para Cp0 (100 K) e para 95 substâncias testadas o desvio médio absoluto percentual (DMA %) é de 25 %. O número de substâncias com desvios superiores a 10 % é de 73 e com desvios < 5% é de 8. Aplicando as contribuições de 2ª ordem sempre que possível (a 24 compostos) obtém-se DMA = 28 %.
(iii) Para Cp0 (298 K) e para 217 substâncias consideradas o desvio médio absoluto percentual (DMA %) é de 3 %. O número de substâncias com desvios superiores a 10 % é de 11 e com desvios < 5% é de 183. Aplicando as contribuições de 2ª ordem sempre que possível (a 67 compostos) obtém-se DMA = 3 %.
(iv) Para Cp0 (700 K) e para 217 substâncias consideradas o desvio médio absoluto percentual (DMA %) é de 2 %. O número de substâncias com desvios superiores a 10 % é de 4 e com desvios < 5% é de 207. Aplicando as contribuições de 2ª ordem sempre que possível (a 68 compostos) obtém-se DMA = 3 %.
(v) Para Cp0 (1000 K) e para 215 substâncias consideradas o desvio médio absoluto percentual (DMA %) é de 2 %. O número de substâncias com desvios superiores a 10 % é de 3 e com desvios < 5% é de 257. Aplicando as contribuições de 2ª ordem sempre que possível (a 66 compostos) obtém-se DMA = 2 %.
BIBLIOGRAFIA
[1] J. D. Cox, D. D. Wagman, V. A. Medvedev, CODATA Key Values for Thermodynamics, Hemisphere Publishing Corp., New York, 1989.
[2] L. Constantinou, R. Gani, AIChE J. 40 (1994) 1697. (ver biblioteca do DEQ)
[3] L. Constantinou, R. Gani, J. P. O' Connell, Fluid Phase Equil. 104 (1995) 11. (ver biblioteca do DEQ)
[4a] Reid, R. C.; Prausnitz J. M; Poling, B. E., " The properties of gases and liquids", 4th Edt.,McGraw-Hill, New York, 1987. (ver biblioteca do DEQ)
[4b] Poling, B. E.; Prausnitz J. M.; O'Connel J. P. " The properties of gases and liquids", 5th Edt.,McGraw-Hill, New York, 2001. (ver biblioteca do DEQ)
EXEMPLO DE APLICAÇÃO
Determinar DHf 0(298.15 K), DGf 0(298.15 K) e Cp0 (700 K) para o 2-etilfenol e comparar com os valores tabelados de -145.23 kJ/mol , -23.15 kJ/mol e 283.14 J/(mol.K).
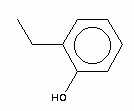
Representação da molécula de 2-etilfenol.
Resolução
Da tabela 2 e reparando na
fórmula estrutural da molécula vemos que têm que ser considerados para as
contribuições de 1ª ordem um grupo CH3, quatro ACH, um ACCH2
e um ACOH. Não há grupos de 2ª ordem a considerar. Podemos então construir a seguinte
tabela seguindo as equações dadas na tabela ao lado da APPLET JAVA:
| Grupo k | Nk | Nkhf 1k | Nkgf 1k | NkCpA1k | NkCpB1k | NkCpC1k |
| CH3 ACH ACCH ACOH |
1 4 1 1 |
-45.947 44.7560 9.4040 -164.6090 |
-8.0300 90.1320 41.2280 -132.0970 |
35.1152 65.5176 32.8206 39.7712 |
39.5923 130.9732 70.4153 35.5676 |
-9.9232 -52.6768 -28.9361 -15.5875 |
| Total | -156.3960 | -8.7670 | 173.2246 | 276.5484 | -107.1236 |
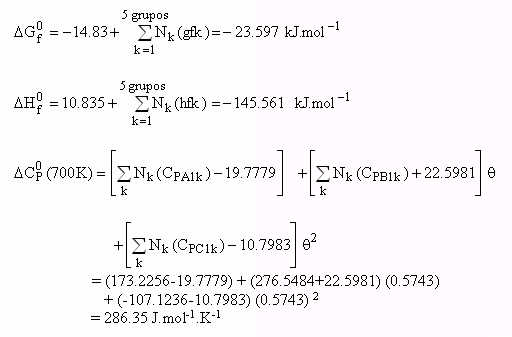
Os desvios percentuais são de 0.23 % para DHf 0(298.15 K), de 1.9 % para DGf 0(298.15 K) e de 1.1 % para Cp0 (700 K).