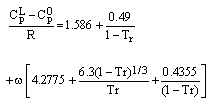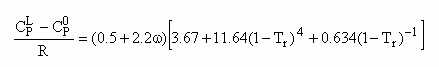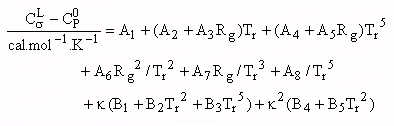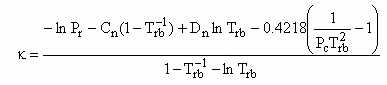ESTIMATIVA
DE PROPRIEDADES TERMOFÍSICAS
Capacidade
calorífica do líquido CpL
INTRODUÇÃO
A necessidade de valores da capacidade calorífica no projecto de unidades
industriais é por demais evidente.
Embora as determinações experimentais desta propriedade possam ser
feitas com grande rigor é impossivel realizar medidas em largos domínios de temperatura
( e pressão ) e para todas as substâncias conhecidas. Por outro lado a precisão
requerida nos processos industriais ronda ± 1 cal / mol / K. Por estes motivos foram propostos diversos métodos de
estimativa da capacidade calorífica de líquidos. Os métodos principais utilizados
dividem-se em dois grandes grupos: (i) os baseados no princípio dos estados
correspondentes (PEC) e; (ii) os de contribuição de grupos. Para uma visão mais
alargada deste assunto veja-se [1].
MÉTODOS
Baseados no PEC:
- Bondi (1966) [2]; Rowlinson (1969) [3];Poling et
al.(2001)[1];Yuan e Stiel (1970) [4]; Lyman e Danner (1976) [5].
Baseados na contribuição de grupos:
- Chueh e Swanson (1973) [6]; Missenard (1965)
[7]; Luria e Benson ( 1977)[8] ; Rùzicka e
Domalski (1993) [9].
Os métodos aqui incluidos são os de (i) Rowlinson e Bondi revisto por
Poling et al., (ii) o Sternling e Brown, (iii) o de Lyman e Danner e (iv) o de
Luria e Benson. Os dois primeiros são de fácil aplicação necessitando de um
reduzida quantidade de informação inicial relativa ao composto em causa e pode
aplicar-se a qualquer composto em princípio. O terceiro utiliza comparativamente pouca
mais informaçao a qual inclui um parãmetro estrutural - o raio de giração da
molécula. O método de Luria e Benson aplica-se a hidrocarbonetos e necessita apenas do
conhecimento da estrutura molecular destes pois trata-se de um método baseado na
contribuição de grupos. Os domínios de temperatura cobertos são mais extensos que no
método de Rùzicka e Domalski. Este último método está limitado à região de
temperatura entre o ponto de fusão e a zona do ponto de ebulição normal (Tb).
O método de Rùzicka e Domalski cobre no entanto uma vasta gama de estruturas
moleculares.
JAVA MÉTODO DE BONDI REVISTO POR POLING et
al. |
|
|
A equação utilizada no cálculo é
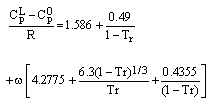
onde :
- CPL
é a capacidade calorifica do líquido à temperatura T;
- Cp0 é a
capacidade calorífica do gás perfeito;
- w é o factor acêntrico
de Pitzer;
- Tr é a temperatura
reduzida (Tr = T / Tc). Tc é a temperatura crítica.
A equação (1) é semelhante á
que foi proposta por Bondi (1968): As constantes foram reajustadas por Poling et al.[1b].
A aplicação da equação (1) efectuada por estes autores a 212 substâncias puras
indica que os desvios percentuais entre os valores calculados e experimentais de Cp são
cerca de 10% para 18 substâncias que formam pontes de hidrogénio ou que dimerizam.
Para as restantes 194 substâncias o desvio médio percentual não ultrapassava 2.5 %. |
JAVA / MÉTODOS: (i) DE DE BONDI REVISTO POR POLING et al.;(ii)
De STERNLING E BROWN; (iii) DE LYMAN E DANNER |
|
|
A equações
utilizadas no cálculo são:
(i) no método de Bondi e Rowlinson revisto por Poling et al foram dadas
na applet anterior;
pode efectuar aqui os cálculos ou na applet anterior.
(ii) no método de Sternling e Brown
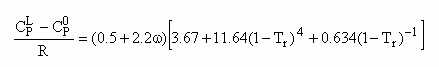 onde:
- CPL é a capacidade calorifica do líquido à temperatura T;
- Cp0 é a capacidade calorífica do gás perfeito;
- w é o factor acêntrico de Pitzer;
- Tr é a temperatura reduzida (Tr = T / Tc). Tc é a temperatura crítica;
Este método é analíticamente semelhante ao de Bondi e Rowlinson revisto por Poling et
al. mas fornece estimativas da capacidade calorífica geralmente diferentes daquele
método.
(iii) no método de Lyman e Danner
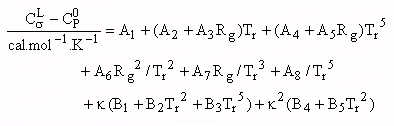
onde:
- CsL
é a capacidade calorifica do líquido saturado à temperatura T;
- Cp0 é a capacidade calorífica do gás perfeito;
- Rg é o raio de giração da molécula (ver tabela A anexa)
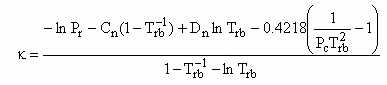
onde Trb=Tb/Tc (Tb é a temperatura de ebulição
normal) e os parâmetros Cn e Dn são:

|
JAVA
MÉTODO DE LURIA E BENSON |
|
|
No método de Luria e Benson tal como
em qualquer método de contribuição de grupos cada grupo na molécula contribui com um
valor bem definido para a capacidade calorífica do líquido, independente do valor dos
outros grupos. As contribuições dos diferentes grupos e as contribuições
estruturais são representadas por polinómios do tipo
CP(L) grupo = A + BT + CT2
+ DT3
Luria e Benson examinaram
1209 valores de CpL encontrando um desvio padrão e desvio médio
percentual entre os valores calculados e experimentais de 0.8 e 0.64 cal mol-1
K-1 respectivamente.
Como exemplo de cálculo tomemos
o 1,4-pentadieno C5H8 cuja estrutura é
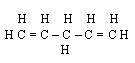
Os grupos envolvidos são: 2 grupos Cd(Cd)(H)2 (f) - Um carbono de
ligação dupla, Cd, está ligado a outro carbono de ligação dupla (Cd) e a dois átomos
de hidrogénio (H)2 ; 2 grupos Cd(Cd)(C)(H) (g) - Um carbono de ligação dupla, Cd, está
ligado a outro carbono de ligação dupla (Cd), a um átomo de carbono (C) e a um átomo
de hidrogénio (H); 1 grupo C(Cd)2(H)2 (l) - Um carbono de ligação de ligação simples
C, está ligado a dois carbonos de ligação dupla (Cd) e a dois átomos de hidrogénio
(H)2. Outras estruturas podem ser analisadas de modo idêntico |
BIBLIOGRAFIA
[1a]
Reid, R. C.; Prausnitz J. M; Poling, B. E., " The properties of gases and
liquids",
4th Edt.,McGraw-Hill, New York, 1987.
[1b]
Poling, B. E.; Prausnitz J. M.; O'Connel J. P. " The properties of gases and
liquids",
5th Edt.,McGraw-Hill, New York, 2001.
[2]
Bondi, A. Ind. Eng. Chem. Fundam.5 (1966) 443.
[3]
Rowlinson, J. S. "Liquids and liquid mixtures", 2d. Edt., Butterworth, London,
1969.
[4]
Yuan, T.-F.; Stiel L. I., Ind. Eng. Chem. Fundam. 9 (1970) 393.
[5]
Lyman, , T. J.; Danner, R. P. AIChE J. 22 (1976) 759.
[6]
Chueh, C. F.; Swanson, A. C., Chem. Eng. Prog. 69 (1973) 83.
[7]
Missenard, F.-A., C. R. 260 (1965) 5521.
[8]
Luria, M.; Benson, S. W. J. Chem. Eng. Data 20 (1977) 90.
[9]
Rùzicka, V.; Domalski, E. S., J. Phys. Chem. Ref. Data 22 (1993) 597, 619.
DADOS SOBRE CpL
| Zábranský, M. V.; Rùzicka, Majer, V.; Domalski, E. S."Heat
capacity of liquids:critical review an recommended values", Amer. Chem. Soc./ Amer.
Inst. Phys. For NIST, Washington D. C., 1996. (Bib. DEQ) |
Compilação de valores da capacidade calorífica do líquido para
1600 substâncias. |
| Domalski, E. S.; Hearing, E. D., J. Phys. Chem. Ref. Data, 25
(1996) 1 (Bib. DEQ) |
Valores a 298.15 K de 2500 substâncias. |
| Daubert, T. E.; Danner R. P.; Sibel, H. M.; Stebbins, C. C.,"Physical
and thermodynamic properties of pure chemicals: data compilation", Taylor &
Francis, Washington D. C., 1997. (1997) |
Equações do cálculo de CpL. |