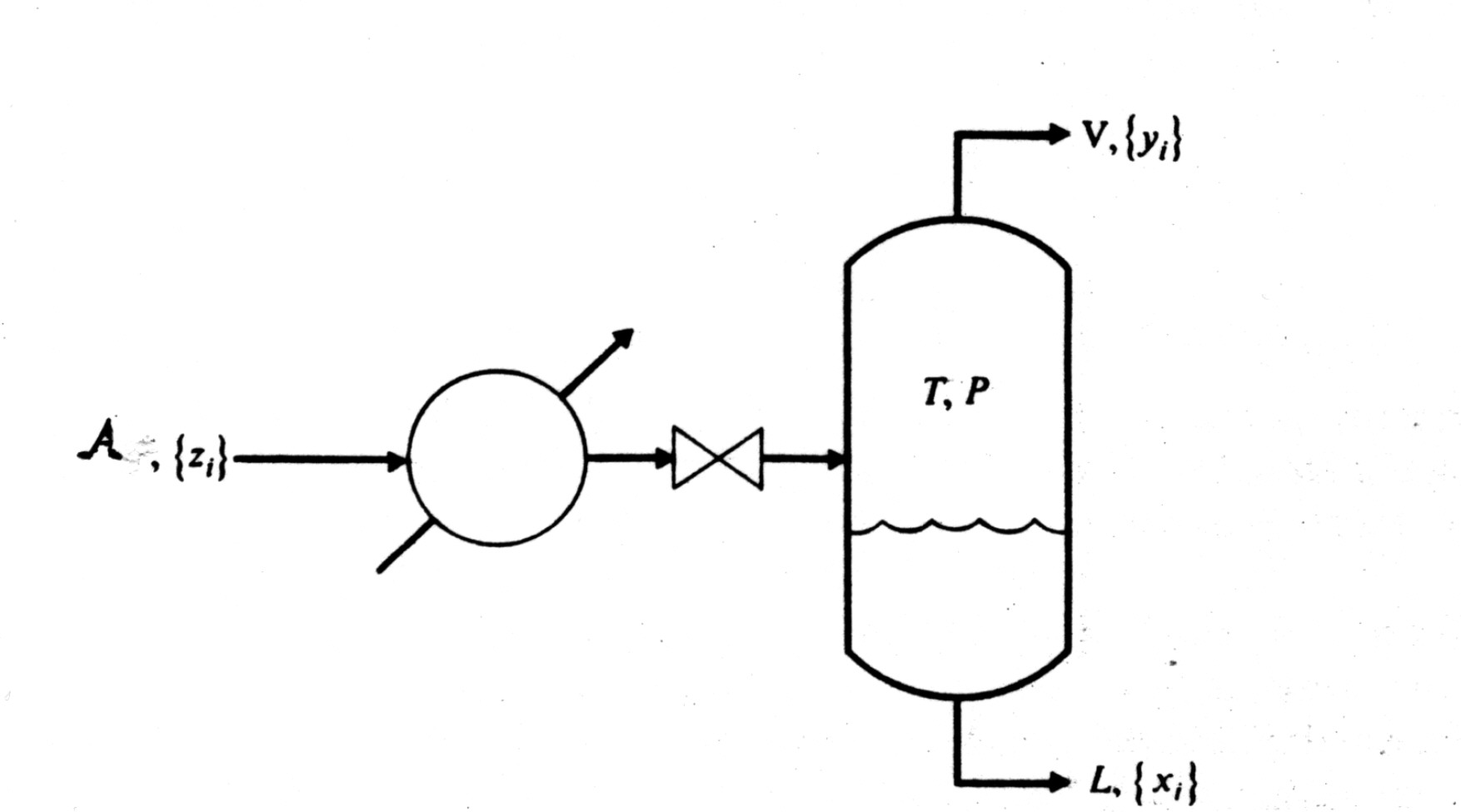
O enquadramento do problema do cálculo FLASH em engenharia em termos das variáveis pressão, temperatura e composição das fases em equilíbrio pode compreeender-se observando o esquema seguidamente apresentado.

Uma corrente A, de alimentação, formada por N componentes, dá entrada num separador líquido-gás, que opera à pressão P e à temperatura T. A composição da corrente de alimentação é dada pela fracção molar zi de cada um dos componentes designados por { zi} , i= 1,2, ,N. No separador atinge-se o estado de equilíbrio à pressão P e à temperatura T, sendo a composição do líquido { xi} , i= 1,2, ,N e a do vapor { yi} , i= 1,2, ,N. Designemos por L e por V as quantidades de líquido e de vapor formados nestas condições. Num cálculo FLASH comum são conhecidos o caudal A, { zi} (i= 1,2, ,N) , P e T e as incógnitas são V (ou L), { xi} , (i= 1,2, ,N) e { yi} , (i=1,2, ,N).
Sem perda de generalidade, podemos tomar A=1 mol. O balanço global ao separador virá então
e, o balanço ao componente i genérico, é
Convém introduzir neste ponto a relação
que designaremos por constantes de equilíbrio da vaporização do componente i. Aplicando (1) e (3) a (2) ter-se-á
quer dizer
| ... (i=1,2, ,N) , (4) |
ou, tendo em conta que L= 1-V
| ... (i=1,2, ,N) .(5) |
Tendo em consideração que xi = yi / Ki , obtém-se de (4) e de (5) que
| ... (i=1,2, ,N) , (6) |
ou,
| ...(i=1,2, ,N) .(7) |
Introduzindo as retrições å xi =1 e å yi =1, às relações (4) a (7) temos que
| ... (i=1,2, ,N) ,(8) |
| ... (i=1,2, ,N) .(9) |
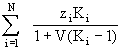 | =1 ... (i=1,2, ,N) , (10) |
| =1 ... (i=1,2, ,N) .(11) |
Uma vez conhecidos os Ki o cálculo de V (ou de L) pode ser efectuado com qualquer das equações anteriormente encontradas. No entanto para evitar problemas numéricos no cálculo tem sido sugerida a utilização de uma combinação destas equações: por exemplo subtraindo (8) a (10) obtém-se de imediato
| ... (i=1,2, ,N) ,(12) |
que é da forma F(V) = 0 , sendo
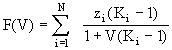 | . (13) |
Subtraindo (9) a (11)
| ... (i=1,2, ,N) .(14) |
que é da forma F(L) = 0, onde
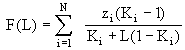 |
As equações (12) ou (14) são sempre monótonas em V (ou L) ao contrário das equações (8) a (11). Para encontrar a solução (valor de V) de (12) ou de (14) (valor de L) utiliza-se um método de pesquisa de zeros (por exemplo o algoritmo de Newton-Raphson). De (13) obtém-se que
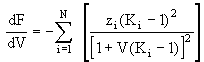
o que significa que F é monótonamente decrescente no intervalo 0<V<1. Consequentemente a existência de duas fases em equilíbrio (0<V<1) só é possível desde que F(V=0)>0 e F(V=1)<0. Como fácilmente se pode verificar
|
|
Podemos considerar os seguintes casos:
Estes casos estão resumidos na Tabela 1 e na Figura 1.
| Características físicas da equação geral | 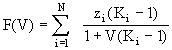 |
|
Caso |
Estado |
F(V=0) |
F(V=1) |
|
1 |
Gás sobreaquecido |
>0 |
>0 |
|
2 |
Ponto de orvalho |
>0 |
=0 |
|
3 |
L+G |
>0 |
<0 |
|
4 |
Ponto de ebulição principiante |
=0 |
<0 |
|
5 |
Líquido sobrearrefecido |
<0 |
<0 |
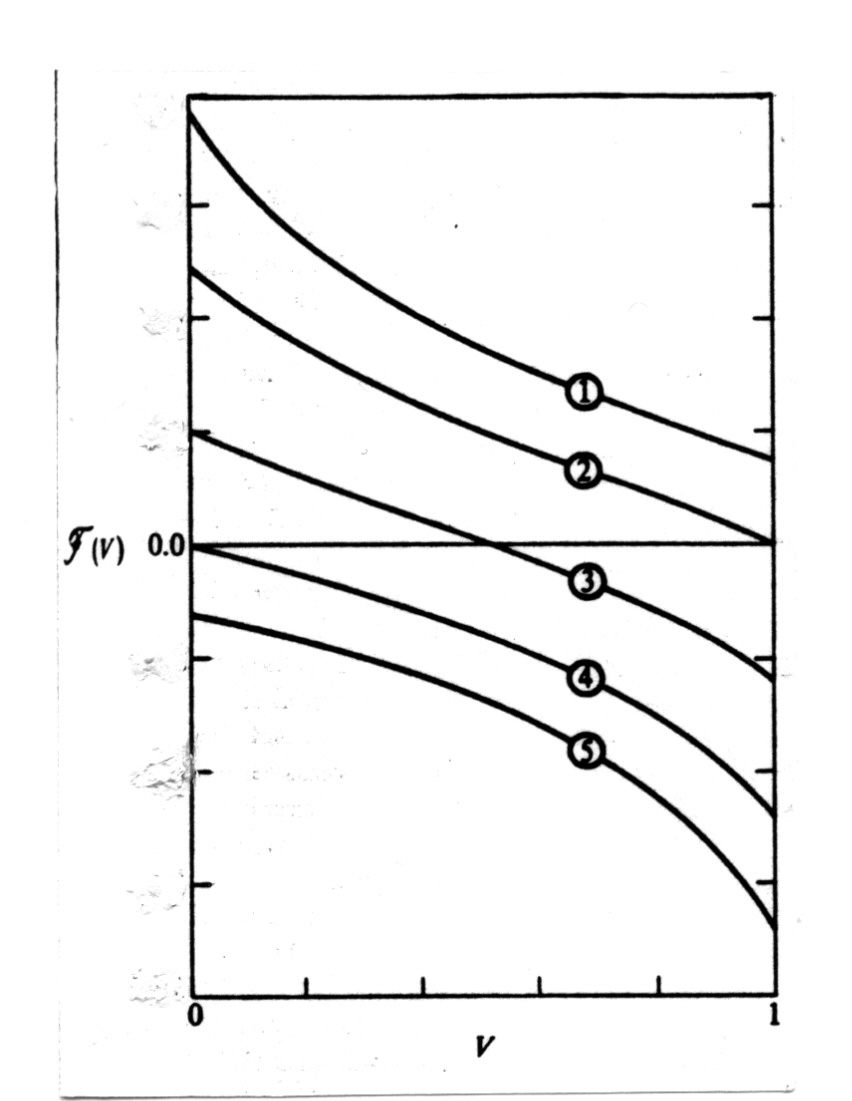
| Figura 2 - Características físicas da equação geral | 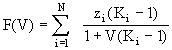 |
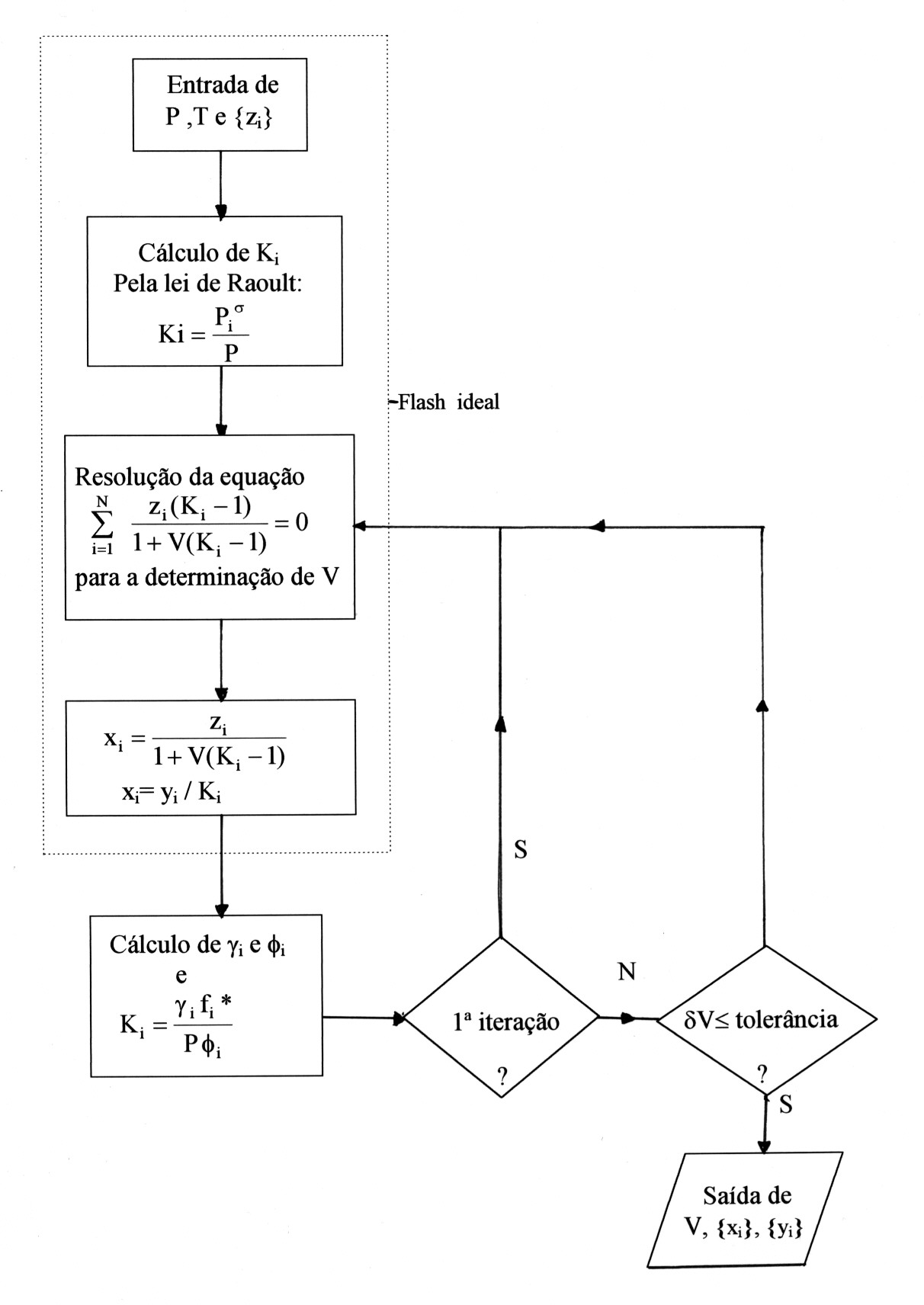
Apresenta-se a seguir um fluxograma para o cálculo flash.A zona indicada a tracejado corresponde ao caso da aplicação da lei de Raoult .