PRESSÃO DE VAPOR DE LÍQUIDOS

Designa-se por vaporização (ou evaporação) o processo segundo o qual um líquido é convertido no vapor. O fenómeno inverso chama-se condensação. Ambos os fenómenos ocorrem à superfície do líquido.

Num líquido, as moléculas com maior energia cinética à superfície escapam-se da superfície do líquido formando a fase gasosa. Algumas moléculas mais lentas da fase gasosa e nas proximidades da fase líquida, têm um trajecto oposto, passam à fase líquida.

Num vaso fechado onde se tenha efectuado o vazio, a vaporização do líquido vai tendo lugar até  que a certa altura, quando a pressão no interior do vaso atinge um valor máximo, as moléculas regressam à fase líquida de tal modo que a  velocidade de retorno das moléculas ao líquido é igual à velocidade da sua vaporização. Quer dizer é estabelecido um equilíbrio dinâmico entre o líquido e o seu vapor em que a vaporização e a Condensação ocorrem à mesma velocidade.

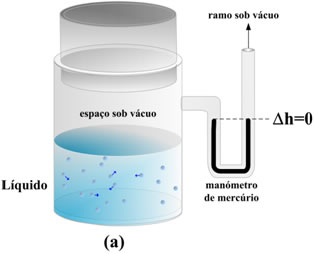
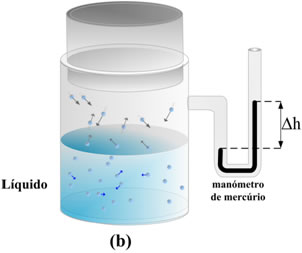
Figura 1 Ilustração dos conceitos de vaporização e pressão de vapor. (a) O espaço acima da superfície do líquido está sob vácuo bem como o ramo direito do manómetro de mercúrio; (b) a vaporização do líquido tem lugar e passado algum tempo a velocidade de saída das moléculas do líquido iguala a velocidade com que estas regressam ao líquido vindas da fase gasosa. O resultado é a existência permanente de moléculas na fase gasosa que provocam uma pressão que se verifica através do desnível no manómetro de mercúrio. Essa pressão é a pressão de vapor.

 As moléculas que escaparam da fase líquida que formam a fase gasosa, como no caso de qualquer gás exercem uma pressão. A pressão estabelecida no vaso (fechado) designa-se por pressão de vapor e o seu valor é função da temperatura. Podemos assim definir uma relação entre as variáveis temperatura, T, e pressão, P, a que tem lugar o equilíbrio dinâmico, relação que será do tipo P=F(T). Essa relação pode ser representada graficamente segundo uma curva contínua no plano (T, P), designada por curva da pressão de vapor (ou de vaporização). Daqui para diante a pressão de vapor de uma substância pura será designada por Pσ (a letra grega σ designa condições de vaporização no equilíbrio dinâmico e o asterisco, *, designa substância pura).

Ebulição
Num vaso aberto para a atmosfera, fornecendo calor ao líquido aumentamos a sua temperatura e desta forma cada vez mais moléculas do líquido passam á fase gasosa por evaporação. A determinada altura observa-se a formação de bolhas no interior do líquido e esse processo torna-se cada vez mais violento: as bolhas de vapor formam-se no interior do líquido e rebentam á superfície aumentando a quantidade de matéria na fase gasosa à custa do líquido. Diz-se que o líquido entrou em ebulição. Isto acontece quando a pressão de vapor (referida no caso do vaso fechado) é igual à pressão ambiente (ou exterior) que está exercida sobre o líquido. Na ebulição, a vaporização ocorre não apenas à superfície do líquido mas também, de forma violenta, no seu interior. A Figura 2 ilustra algumas das diferenças fundamentais entre os fenómenos da vaporização e da ebulição.

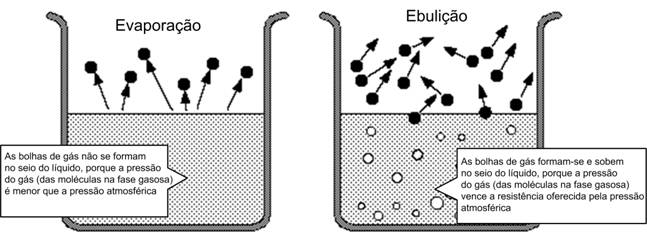
Figura 2. Vaporização e ebulição.

Variando a pressão externa exercida sobre a superfície do líquido vamos ter temperaturas diferentes a que o líquido entra em ebulição ou por outras palavras a temperatura de ebulição de um líquido depende da pressão exterior que é exercida sobre ele.

Quando a pressão externa aplicada ao líquido é igual a 1 atm falamos em ebulição normal e em temperatura de ebulição normal (designada por Tb). Por exemplo para a água é Tb=100ºC. Quer dizer, um líquido entra em ebulição a diferentes temperaturas conforme se faça variar a pressão externa exercida no líquido. A relação entre a temperatura a que se observa a ebulição e a pressão exercida é a mesma função Pσ=F(T) correspondente à curva de vaporização referida anteriormente (para o vaso fechado). Assim, o ponto de ebulição normal referido atrás, mais não é que o ponto da curva de vaporização de uma substância pura onde (T= Tb e Pσ=1 atm).

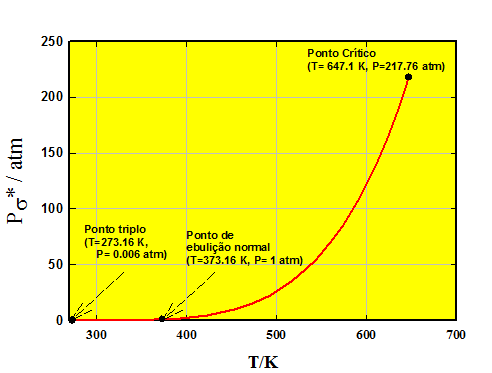Figura 3 Ilustração do ponto triplo. Gelo (iceberg) coexistindo com o líquido no qual flutua, e com a fase gasosa (ar e vapor de água).	Figura 4. Ilustração da curva da pressão de vapor da água (H2O) assinalando-se pontos notáveis situados na mesma. A curva de vaporização tem o seu início no ponto triplo (situação em que coexistem a substância sólida (s), líquida (l) e gasosa (g)) e termina no ponto crítico (c) onde as fases líquida e gasosa são praticamente indistinguíveis.

O intervalo de temperatura em que uma substância existe como um líquido - a partir da temperatura do ponto triplo até à temperatura do ponto crítico é geralmente determinado pelo tamanho, forma e polaridade das moléculas. As moléculas pequenas, apolares tendem a ter temperaturas críticas baixas. O aumento do tamanho e da polaridade tendem a elevar a temperatura crítica de uma série de moléculas de formas semelhantes. A capacidade de um composto para formar ligações por pontes de hidrogénio entre as moléculas aumenta o valor da temperatura crítica. A influência na temperatura de ebulição explica-se essencialmente da mesma maneira.

A inclinação da curva da pressão de vapor (entre as fases líquido e vapor) está intimamente relacionada com a quantidade de energia necessária para converter o líquido em vapor . Essa quantidade é a entalpia de vaporização. A inclinação da curva da pressão de vapor a uma dada temperatura T (que matemáticamente corresponde à derivada dPσ/dT) é equivalente ao valor da tangente do ângulo que a reta tangente à curva de vaporização a T faz com o eixo horizontal (ou da temperatura). esta inclinação relaciona-se com a entalpia de vaporização e com a variação de volume na vaporização através da equação de Clapeyron:

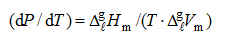     (A)

onde

 sendo Vmg o volume (molar) do gás e Vmℓ o volume molar do líquido em equilíbrio com o gás (ou vapor).

A temperaturas suficientemente inferiores à temperatura crítica (T<<Tc):

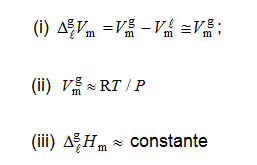
Com estas condições a equação de Clapeyron (A) vem:

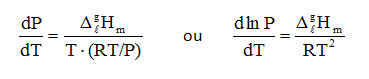      (B)

Partindo da equação (B) e considerando a hipótese (iii) anterior pode encontrar-se que

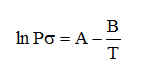    (C)

A equação (C) mostra duas coisas:
       (i) a relação entre o logaritmo da pressão de vapor e o inverso da temperatura é linear; e
       (ii) aplicando a equação (B) obtém-se que

A entalpia de vaporização pode obter-se a partir da equação da recta  ln(Pσ/) em função de 1/T.   Para tal basta ter alguns valores da pressão de vapor em função da temperatura.

Embora a equação (C) seja uma aproximação simples e razoável da pressão de vapor observada como uma função da temperatura, a maioria dos compostos apresentam curvatura definida quando se representa o logaritmo natural da pressão de vapor em função do inverso da temperatura absoluta, 1 / T.  Esta curvatura é devida ( principalmente) ao afastamento do comportamento de gás perfeito por parte do vapor e da variação da entalpia de vaporização com a temperatura.