- Polinómio Interpolador de Lagrange

Dados n+1 pontos  o polinómio de interpolação de Lagrange é dado por:

 

 

          

 

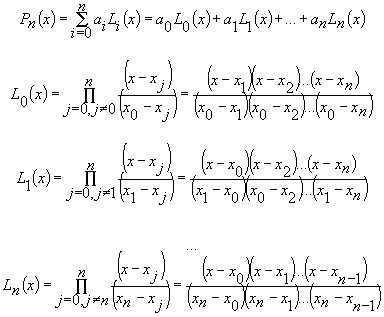
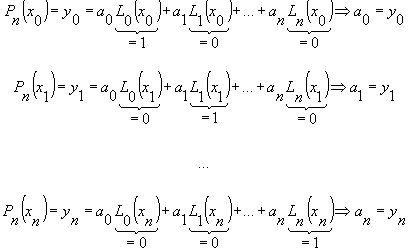
Assim, o polinómio de Lagrange toma a forma:

 

 

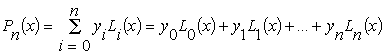
Exemplo:

X     f(x)

X₀      f₀

X₁      f₁

X₂      f₂

X₃      f₃

 

                O polinómio de Lagrange pode ser utilizado para pontos irregularmente espaçados. Assim, para este caso a equação toma a seguinte forma:

 

 

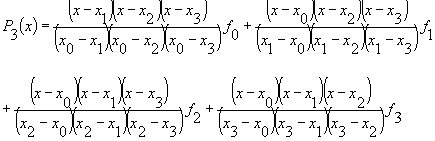
          É  de notar que esta equação é formada por quatro pontos, no entanto, o grau do polinómio é de ordem três. No numerador, cada termo é constituído, como um produto de factores lineares da forma  omitindo um x_i em cada termo. O valor omitido é usado para formar o denominador substituindo x em cada factor do numerador. Cada termo é multiplicado por f_i correspondente ao x_i omitido nos factores do numerador.

          Para a formulação de polinómios de Lagrange de outras ordens segue-se o mesmo esquema de raciocínio. A resolução aritmética deste processo é bastante vagarosa pelo que um programa computacional que implemente o método facilita esta tarefa.

Uma interpolação polinomial quando passa pelos pontos usados na sua construção não fornece os valores correctos quando é usada para interpolação, pelo que é do nosso interesse avaliar o erro de interpolação.

 

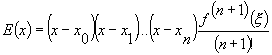
 em que  pertence ao intervalo que contém .

          Esta expressão do erro é bastante interessante, mas não é de grande utilidade já que a função f é geralmente desconhecida e assim não é possível saber as (n+1) derivadas. No entanto, se se tratar de uma função ‘suave’ um polinómio de baixo grau adapta-se satisfatoriamente, por outro lado, uma função ‘não suave’ apresentará elevados erros de interpolação.