- Polinómio Interpolador de Newton
Este método é baseado numa aproximação linear de uma função fazendo
uma tangente à curva (fig.1).
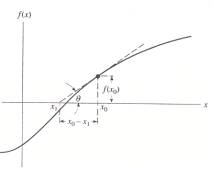
Fig.1 – Representação gráfica da tangente à curva da função f.
Partindo de uma estimativa inicial x0 (cujo valor não se
afasta muito da raiz da função) percorre-se a tangente até à sua intersecção
com o eixo dos xx e toma-se esse valor para a seguinte aproximação. Este
processo continua até que os sucessivos valores do eixo do xx sejam
suficientemente próximos, ou até o valor da função se aproximar de zero.
A sua fórmula é obtida a partir da construção sucessiva de polinómios de graus inferiores. Para estabelecer essa fórmula convém introduzir a noção de diferença dividida.
A diferença
dividida de 1ª ordem é definida de uma forma geral por:
f [ xi, xj] = ( fi - fj
) / ( xi - xj )
e uma diferença dividida de ordem k,
pode ser obtida a partir das anteriores :
f [ xi , ... , xi+k]
= ( f [ xi+1, ... , xi+k ] - f [ xi, ... , xi+k-1
] ) / ( xi+k - xi )
Pode-se agora escrever a fórmula de Newton:
pn(x) = pn-1(x) + f [ x0 , ... , xn ] (x - x0) ... ( x - xn-1)
e podemos obter
sucessivamente, a partir do polinómio interpolador de grau zero p0(x)
= f0 :
p1(x) = f0 + f [ x0 ,
x1 ] ( x - x0)
p2(x) = f0 + f [ x0 , x1 ] ( x - x0)
+ f [ x0 , x1, x2 ] ( x - x0) ( x -
x1)
... etc ...
Assim, a
fórmula de Newton é dada por:
![]()
-
Erro na interpolação polinomial de Newton:
O polinómio de grau n obtido, fn(x), é semelhante à
expansão em série de Taylor mas não é exactamente igual à verdadeira função
devido ao erro de truncatura.
f(x) = fn(x) + Rn
onde Rn
é o erro de truncatura e é dado por
![]()
em que f(n+1) é a (n+1) derivada.
A equação anterior é semelhante à expressão do erro de truncatura da série
de Taylor. Para o seu cálculo é necessário conhecer a função e ela ser
derivável, o que muitas vezes não acontece. Nesses casos, aproxima-se a
derivada de ordem (n+1) pelo quociente de diferenças (“diferenças divididas”).
Assim, o erro vem:
![]()
mas neste caso Rn também contém a função desconhecida
f(x), então substitui-se x por um ponto adicional xn+1.[...]
Agora o erro será aproximadamente:
![]()
como este Rn não é o
verdadeiro erro, não se pode afirmar que
f(x)= fn(x) + Rn
mas pode-se concluir que
fn+1(x)= fn(x) + Rn