(f11 * f22)/(f12 * f21)
where fij represents the respective frequencies in the 2x2 table.
On-Line Analytic Processing (OLAP) (or Fast Analysis of Shared Multidimensional Information - FASMI). The term On-Line Analytic Processing refers to technology that allows users of multidimensional data bases to generate on-line descriptive or comparative summaries ("views") of data and other analytic queries.
For more information, see On-Line Analytic Processing (OLAP); see also, Data Warehousing and Data Mining techniques.
One-of-N Encoding. Representing a nominal variable using a set of input or output units, one unit for each possible nominal value. During training, one of the units will be on and the others off.
One-Off. A case typed in and submitted to the neural network as a one-off procedure (not part of a data set, and not used in training).
Ordinal Scale. The ordinal scale of measurement represents the ranks of a variable's values. Values measured on an ordinal scale contain information about their relationship to other values only in terms of whether they are "greater than" or "less than" other values but not in terms of "how much greater" or "how much smaller."
See also, Measurement scales.
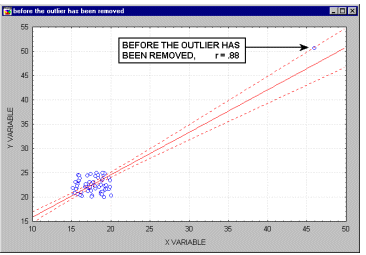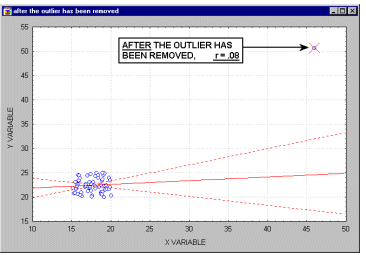
Outliers. Outliers are atypical (by definition), infrequent observations. Because of the way in which the regression line is determined in Multiple Regression (especially the fact that it is based on minimizing not the sum of simple distances but the sum of squares of distances of data points from the line), outliers have a profound influence on the slope of the regression line (see the animation below) and consequently on the value of the correlation coefficient. A single outlier is capable of considerably changing the slope of the regression line and, consequently, the value of the correlation. Note, that as shown on that illustration, just one outlier can be entirely responsible for a high value of the correlation that otherwise (without the outlier) would be close to zero. Needless to say, one should never base important conclusions on the value of the correlation coefficient alone (i.e., examining the respective scatterplot is always recommended).

Note that if the sample size is relatively small, then including or excluding specific data points that are not as clearly "outliers" as the one shown in the previous example may have a profound influence on the regression line (and the correlation coefficient). This is illustrated in the following example where we call the points being excluded "outliers;" one may argue, however, that they are not outliers but rather extreme values.
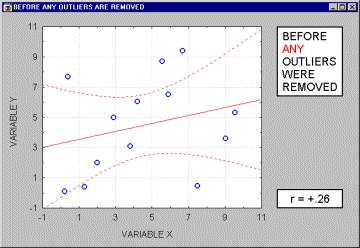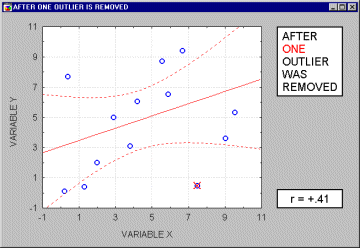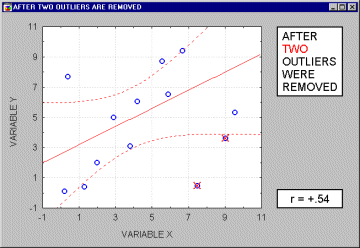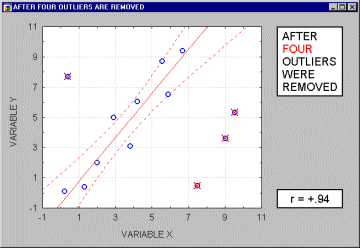
Typically, we believe that outliers represent a random error that we would like to be able to control. Needless to say, outliers may not only artificially increase the value of a correlation coefficient, but they can also decrease the value of a "legitimate" correlation.
See also Confidence Ellipse.
Outliers (in Box Plots). Values which are "far" from the middle of the distribution are referred to as outliers and extreme values if they meet certain conditions.
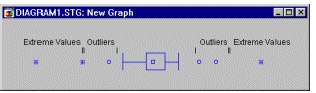
A data point is deemed to be an outlier if the following conditions hold:
data point value > UBV + *o.c.*(UBV - LBV)
or
data point value < LBV - *o.c.*(UBV - LBV)
where
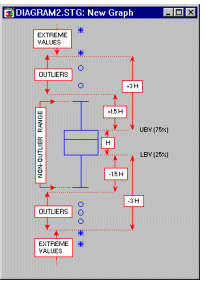
UBV is the upper value of the box in the box plot (e.g., the mean + standard error or the 75th percentile).
LBV is the lower value of the box in the box plot (e.g., the mean - standard error or the 25th percentile).
o.c. is the outlier coefficient.
For example, the following diagram illustrates the ranges of outliers and extremes in the "classic" box and whisker plot (for more information about box plots, see Tukey, 1977).
Overfitting. When attempting to fit a curve to a set of data points, producing a curve with high curvature which fits the data points well, but does not model the underlying function well, its shape being distorted by the noise inherent in the data.
See also, Neural Networks.
Overlearning. When an iterative training algorithm is run, overfitting which occurs when the algorithm is run for too long (and the network is too complex for the problem or the available quantity of data).
See also, Neural Networks.
