Método
da Bissecção
Algoritmo:
Para k=0,1,... fazer:
![]()
![]() então Raiz=xk+1® STOP
então Raiz=xk+1® STOP
Se f(ak)*f(xk+1)<0 então fazer ak+1=ak
e bk+1=xk+1
Se f(bk)*f(xk+1)<0 então fazer ak+1=xk+1
e bk+1=bk
Método
da falsa Posição
Algoritmo:
Inicialização:
a0=a, b0=b e x0=b
Para
k=0,1,... fazer:
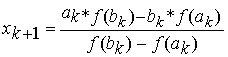
Se
![]() então Raíz=xk+1® STOP
então Raíz=xk+1® STOP
Se
f(ak)*f(xk+1)<0 então fazer ak+1=ak
e bk+1=xk+1
Se
f(bk)*f(xk+1)<0 então fazer ak+1=xk+1
e bk+1=bk
Método da Falsa Posição Modificado
Algoritmo:
Inicialização:
a0=a, b0=b e x0=b, FA=f(a) e FB=f(b)
Para
k=0,1,... fazer:
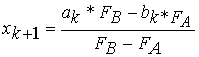
Se
se verificar critério de paragem então ®
STOP; Raíz=xk+1
Se
f(ak)*f(xk+1)<0 então fazer ak+1=ak
e bk+1=xk+1 e FB=f(xk+1)
Se também f(xk)*f(xk+1)>0 fazer FA=FA/2
Se
f(bk)*f(xk+1)<0 então fazer ak+1=xk+1
e bk+1=bk e FA= f(xk+1)
Se também f(xk)*f(xk+1)>0 fazer FB=FB/2
Método
da Secante
Algoritmo:
Iniciação:
x-1e x0
Para
k=0,1,... fazer:
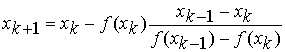
![]() então Raíz=xk+1
então Raíz=xk+1
Inicialização:
x0
Para
k=0,1,... fazer:
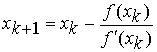
Se
se verificar critério de paragem então ®
STOP; Raíz=xk+1
Método
de Richmond
Algoritmo:
Inicialização:
x0
Para
k=0,1,... fazer:
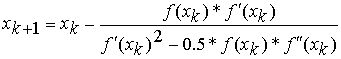
Se
se verificar critério de paragem então ®
STOP; Raíz=xk+1
Método
das Substituições Sucessivas
Inicialização:
x0
Para
k=0,1,... fazer:
![]()
Se
se verificar critério de paragem então ®
STOP; Raíz=xk+1
Inicialização:
xk-1, xk e xk+1
Para
k=0,1,... fazer:
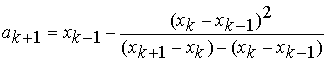
Se
se verificar critério de paragem então ®
STOP; Raíz=xk+1
É
de esperar que ak+1 constitua uma melhor aproximação para a
raíz do que xk+1
Método
de Steffensen
Algoritmo:
Inicialização:
x0
Para
k=0,1,... fazer:
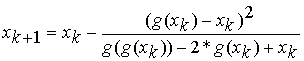
Se
se verificar critério de paragem então ®
STOP; Raíz=xk+1
Método
de Muller
Algoritmo:
Inicialização:
h1=x1-x0, h2=x0-x2
e g=h2/h1.
Sendo x2<x0<x1 e f0=f(x0),
f1=f(x1) e f2=f(x2)
Nova
aproximação para a raíz:
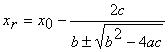
Se
b>0 escolher o sinal +, se b<0 escolher o sinal -, se b=0 é indiferente.
Os parâmetros a, b e c são definidos do seguinte modo:
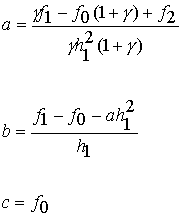
Se
xr>x0 fazer (x0, xr, x1)® (x2, x0, x1).
Se
xr<x0 fazer (x2, xr, x0)
® (x2, x0, x1).
Clique Aqui para aceder à representação gráfica de alguns métodos.