Resolução de Equações não lineares

        Embora muitos dos problemas que surgem no dia a dia possam ser   expressos por equações lineares do tipo f(x) = a + bx e resolvidos através dos seus métodos de resolução, outros há em que estas equações não se aplicam.

       A  resolução de equações não lineares consiste em determinar os valores x que tornam nulo o valor da função f, ou seja, resolver a equação f(x) = 0.

       Quando a função não linear for do 2.º grau, f(x) = ax²+bx + c, podemos resolvê-la através da Fórmula Resolvente que nos dá duas raízes:

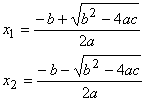
         Há diferenças fundamentais entre equações lineares e não lineares. Em primeiro lugar, nenhum sistema não singular de equações lineares tem uma solução única. Tal não é verdade para equações não lineares (podem não haver soluções reais). Em segundo lugar, um sistema de equações lineares pode ser resolvido usando diversos métodos como é descrito em Equações Lineares, enquanto que no caso das equações não lineares só certas equações é que podem ser resolvidas.

        Os métodos de resolução de equações não lineares podem ser iterativos, construindo uma série de soluções aproximadas, x₁, x₂,...,x_n, x_n+1, da equação f(x) = 0. Não é possível prever à partida que o método converge para uma solução aproximada da equação não linear. Por outro lado, se conhecermos pontos a e b que satisfazem f(a).f(b) < 0, será possível garantir a convergência e também o número máximo de iterações requeridas para estimar a precisão desejada.

        Quando em vez de termos equações tivermos sistemas de equações não lineares, a situação é mais difícil. Tal como atrás, não há soluções ou soluções múltiplas. Não há nenhum algoritmo geral capaz de determinar a solução num tempo finito e então devemos aceitar soluções aproximadas como substituição. no entanto é mais difícil garantir a convergência da solução e a sua existência de um sistema de equações do que quando se trata de uma simples equação.

        Os métodos de resolução dos problemas devem ser iterativos. Cuja forma geral é x_k+1 = f(x_k)   k = 0, 1,2....

        Os métodos de resolução de equações  não lineares podem ser:

 q       Métodos de intervalo

•      Método da bissecção;

•      Método da falsa posição;

•      Método da falsa posição modificado;

•      Método de Muller;

    q   Métodos abertos

•      Método da secante;

•       método de Newton;

•      Método de Richmond;

•      Método das substituições sucessivas;

•      Método de Steffensen;

     Método da Bissecção

      É um dos mais simples métodos de resolução de f(x) = 0 com f(x) contínua em [a,b], com a<b e f(a).f(b)<0. Quando tal acontece, f(x) muda de sinal no intervalo e podemos dizer que aí existe um zero. Ao aplicarmos este método estamos constantemente a reduzir o intervalo [a,b] sempre que se verifique que f(a_k).f(b_k)<0. a cada iteração, o intervalo é dividido em metade. Temos então um ponto médio, m, e podemos denotar o erro de cada iteração i como ei =m - x*. Para o método da bissecção,

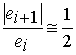
       Sendo p a ordem de convergência e c a razão de convergência então, para qualquer que seja o método de resolução de equações não lineares,

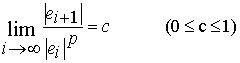
         Cada método tem a sua ordem e razão de convergência. Para o Método da Bissecção, p=1 e c=½. A ordem de convergência assume sempre valores iguais ou superiores a um. Quando p=1 a convergência é chamada linear. Quando p>1 então a convergência é supralinear, havendo o caso especial em que p=2 no qual a convergência é quadrática.

        O Método da Bissecção pode também ser conseguido pela aproximação de f(x) por uma função linear particular a cada iteração e descobrindo os zeros por aproximação linear. A aproximação faz-se por uma recta que passa  pelos pontos (a, sinal f(a)) e (b, sinal f(b)). Se f(a)<0 e f(b)>0,  a recta tem a equação y = -1+2(x-a)/(b-a). Esta é uma aproximação muito imperfeita para f(x) porque ignora os valores da função f(x), tendo somente em atenção os sinais destes. No caso de serem usados os valores da função as aproximações são melhores.

         Esta outra face do Método da Bissecção é considerada por muitos autores como sendo distinta deste método, sendo então denominada por Método da Falsa Posição. Por este método, a solução x_k+1 será a intercepção da recta secante que passa por (a_k, f(a_k))e (b_k, f(b_k)) com o eixo das abcissas.

O Método da falsa posição possui p=1 (convergência linear) e razão de convergência que pode assumir valores superiores ou inferiores a ½ . Em situações de convergência linear, a convergência pode ser muito lenta. No Método da Falsa Posição isto acontece em situações em que a_k ou b_k não variam que é o que sucede em situações em que f(x) é aproximadamente paralela ao eixo das abcissas. Nos casos em que tal acontece, este método pode ser aperfeiçoado de tal modo a que quando as iterações sucessivas se verificam do mesmo lado da raiz, para a iteração seguinte é usado apenas metade do valor da função no extremo oposto do intervalo. A este aperfeiçoamento do Método da Falsa Posição chamamos Método da Falsa Posição Modificado.

 O Método da Secante consiste em fazer uma aproximação linear a f(x) usando duas iterações quaisquer, (x_k, f(x_k)) e (x_k-1, f(x_k-1)) de forma a obtermos o valor x_k+1. A recta secante passa pelos pontos referido e o zero desta recta (sua intersecção com o eixo das abcissas) dá-nos o valor estimado da solução.

Considerando a equação da recta secante que passa pelos pontos (x_k, f(x_k)) e (x_k-1, f(x_k-1)),

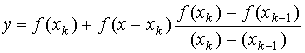
Sendo y = 0 e fazendo x = x_k+1 e reordenando obtemos:

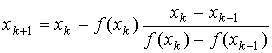
            O Método da Secante não converge sempre e, quando converge, converge supralinearmente com .

 A razão de convergência c será igual a 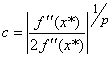em que x* é a solução.

As generalizações do Método da Secante são das mais utilizadas para resolver sistemas de equações não lineares.

Método de Newton

O Método de Newton é assim designado por ter sido sugerido por Newton mas a forma que dele conhecemos é devida a Raphson (1690). Está é um dos melhores métodos de resolução de f(x) = 0. Difere dos métodos referidos anteriormente no sentido em que, em vez de a solução ser calculada por meio de uma secante, é calculada por meio da tangente à curva de f(x). O zero da recta tangente é então a estimativa do valor de x*.

Considerando a equação da Série de Taylor no ponto x_k:

                                                                          f(x) = f(x_k) + f ’(x_k) (x - x_k ) +…

A equação da recta tangente é-nos dada pelos primeiros dois membros da Série de Taylor:

                                                                          y = f(x_k) + f ’(x_k) (x - x_k)

Fazendo y =0 obtemos a fórmula do Método de Newton:

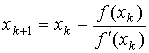
O  Método de Newton é o método muito simpático para se utilizar uma vez que converge rapidamente

 com p=2 (convergência quadrática). Por definição de convergência quadrática,

Tal como acontece também no Método da Secante, o Método de Newton nem sempre é convergente. Por exemplo, quando f’(x_k) = 0, o método não está definido, mantendo-se os problemas para f’(x_k) @ 0. Esta é uma das desvantagens do Método de Newton, sendo outra das suas desvantagens o facto de ter de se calcular derivadas neste método.

Método de Richmond

 Este método consiste num aperfeiçoamento do Método de Newton, convergindo mais rapidamente que este e dando um factor de correcção para a iteração seguinte. As desvantagens na sua aplicação são, à semelhança do que acontece para o Método de Newton, a necessidade do conhecimento das derivadas.

A sua fórmula geral é:

Método das Substituições Sucessivas e Método de Steffensen

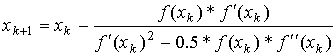
 Estes métodos são idênticos, sendo o Método de Steffensen uma generalização do Método das Substituições Sucessivas. Neste método, em vez de resolvermos  as equações não lineares como f(x)=0, resolvemos x =g(x) que não é mais do que uma outra maneira de escrever f(x)=0. A g(x) damos o nome de fórmula de recorrência que, para uma dada função f(x) não é única, sendo que só algumas interessam para determinar a solução.

O Método das Substituições Sucessivas é convergente desde que se verifique a condição g’(z)<1, sendo essa convergência linear (p=1) e a razão de convergência é dada por c = | g’(x*)|. A convergência pode ser melhorada diminuindo c através da aceleração de Aitken.

O Método de Steffensen é idêntico ao descrito com a diferença de apresentar uma convergência quadrática sempre que g’(z)¹1 pois neste caso a convergência é linear.

Método de Muller

Para além das aproximações por meio de tangentes, secantes ou outras rectas, podemos usar polinómios de ordem superior para essa aproximação. Esta pode ser conseguida considerando aproximações quadráticas, a interpolação quadrática. Podemos aplicá-la quando temos mais do que dois pontos e conseguimos interpolar a curva de f(x) com uma parábola que passa por estes pontos. É neste processo que consiste o Método de Muller. A ordem de convergência neste método é de 1.839, mais elevada do que no Método da Secante.

Critérios de Paragem

Os algoritmos de cada método repetem-se até ao momento em que a tolerância prevista para cada um deles é ultrapassada ou quando um determinado número de algarismos significativos ou casas decimais correctas previamente especificadas não é verificadas. Os casos mais comuns de critérios de paragem dos procedimentos iterativos são a ultrapassagem do número máximo de iterações (n>n_máx) e quando os erros absolutos, relativos ou valor da função ultrapassa a tolerância (tol), ou seja,          

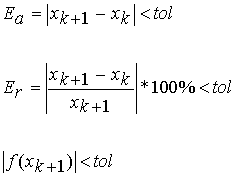
Para ter acesso aos Algoritmos dos Métodos clique Aqui.  

Referências Bibliográficas:

- Kahaner,David; Moler, Cleve; Nash, Stepher; "Numerical Methods and Software", Prentice Hall. 

- Apontamentos das aulas Teórico-Práticas. 

  Retroceder                             Inicio                             Avançar